お世話になります。
新型コロナウイルスが発生して1年と数か月立ちますが、皆さま いかがお過ごしでしょうか。
私は今のところ何とか感染せず生活できております。
感染拡大防止のため 体温観察をしなさい と言われている方も居られるかと思いますが 私も例に漏れず体温を取っております。
今回は体温観察のデータが300日分程度たまりましたので GWの暇つぶしに 品質管理手法を用いて 体温観察の結果を見ていきます。
毒にも薬にもならない話です。暇つぶし程度の内容ですので整合性は追及しないでもらえると助かります。
今回の内容
・使用データについて
・標準偏差と正規分布曲線
・管理図のみかた
使用データについて
以下のデータを使用しています。
実際は2020/3月から体温を測っていましたが しばらくは紙に書いていたので 手元にデータがありませんでした。
管理図の組(群)の数を 7 (1週間)にしたかったのでデータの母数を301日分(43週間)としています。

一応真面目に体温を測っていたつもりでしたが 測り忘れや 休日で朝測れなかった時もありましたので、
有効データ数 朝:284日 夜:300日 としています。
母集団とか分散の扱いは 今後 正規の品質管理記事にも使うことを見越して 雑にしています。
標準偏差と正規分布曲線
データのまとめ方などは 後日記事にしますので 割愛します。
集計の結果 私の朝の体温の平均は 36.48℃、標準偏差は0.113℃になりました。
私の体温が正規分布に従うとすれば、36.48℃を基準として±0.113℃に入る確率は68.26%
36.48℃±(0.133×2)℃に入る確率は95.44%、36.48℃±(0.133×3)℃に入る確率は99.74% になります。
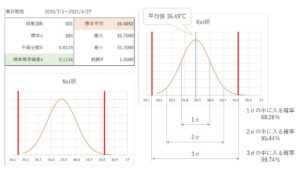
正規分布とは
統計学における連続型確率分布の一つです。
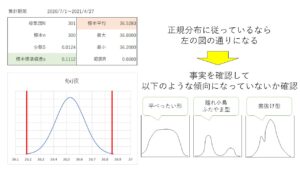
データの平均値付近が頂点となり 平均から離れるにしたがって 発生率が左右対称に低くなっているもの。
左右対称というと三角形も良いのかと思いますが 二次関数のグラフっぽく緩やかに変化するのがポイントです。
多くの統計がこの正規分布に従うことが分かっています。
(体温がそれに従うかはわかりませんし 個人的な感覚では従いません。)
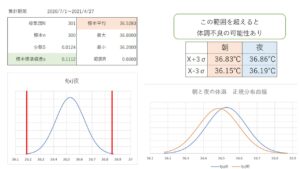
ちなみに私の場合朝と夜を比較すると 平均体温は朝の方が低いっぽいです。
管理図について
体温の場合 平均体温や確率だけでなく 日々の変化が知りたいですよね。
品質管理では傾向値を管理するためのツールとして管理図というものがあります。
管理図は色々な形式のものがありますが 今回は最も代表的な XバーR管理図にまとめてみました。
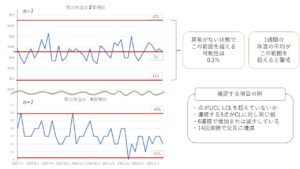
Xバー管理図
普通の折れ線グラフと違い いくつかのデータの平均値をプロットしていく図になります。
今回は1週間(n=7)の体温の平均値を一つのデータとしています。
データが正規分布に従う場合 平均値を中心に傾向無く ばらつきが発生しますので、
一定数が連続して平均値を超えたり、一定数が連続して階段状に増減する場合などは 何かが起こっている可能性が高いです。
ちなみにXバーと書いていますが実際がXの上に横棒が付いた記号です。
Xはデータの数値を、Xバーは数値の平均値を指します。
平均値を集めて平均値の平均値をとったもののことをXバーバー(Xの上に=を付けたもの)と言い標準偏差を計算するのにつかわれたりします)
R管理図
Xバー管理図はデータの平均値を並べたものに対し、R管理図はデータのばらつきを並べた図になります。
今回の場合は 1週間のうち 体温が1番高い時と低い時の差をプロットしています。
1週間でばらつきが大きすぎる場合 逆にばらつきが全くない場合は 何か異常が起きている場合があります。
(品質管理上の考え方であり 多分体温には当てはまりません)
まとめと おわりに
お疲れ様でした。
今回は私の暇つぶしにお付き合いいただきましたが、
データとはそれ1つで効果があるものではなく、集計して、並べて、読み取って、初めて効果があります。
多分ですが品質管理でも 体温観測でも データの特性や 傾向値を管理するということが大事になるかと思います。
今回の正規分布や 標準偏差 、管理図については 技能検定の特級にも出てくる内容ですので 後日 計算の仕方や、より詳しい所を記事にする予定です。
今回は以上になります。
お読みいただきありがとうございました!
ちなみにですが 体温は1日を通して結構変化するそうなので 観測する条件(時間、風呂に入る前後起きてからの経過時間)を
合わせてない場合データとしての信頼性はやや薄くなりそうです。
また年齢や性別などにより個人差や 同じ人でも差がありますのでご注意ください。
特に子どもさんや赤ちゃんはばらつきが大きく、女性(生物学的な)は低温の期間と 高温の期間で 周期がある人もいますので、
実際のデータは正規分布しない可能性が高いです。